1. The travelling security guard

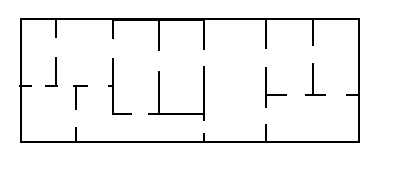
a) A security guard has to go through all rooms of the building (shown to the right) each hour. The question is: Can he make a tour where he visits each room exactly once and ends in the same room (his base) where he starts?

b) Two graphs are associated with this problem. The first, called G₁, has the set of all rooms as vertices, and an edge between two rooms if it is possible to go from one room directly to the other. Draw G₁.

c) The second graph is called G₂. It has the same vertex set as called G₁, but now two vertices are adjacent if the two rooms have some common wall. Draw G₂.

d) Does G₁ have a Hamiltonian cycle? Why or why not?

e) Does G₂ have a Hamiltonian cycle? Why or why not?

f) Answer question (a).

g) If such a tour is impossible, could the guard solve his problem by making some additional doors between rooms? If, how many additional doors does he have to create?

h) Answer questions (a) - (f) for the floorplan shown to the right.

i) Answer questions (a) - (f) for the floorplan shown to the right.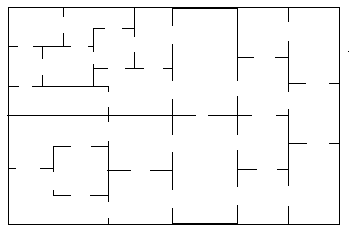

j) Can you generalize your findings in (h) and (i)? If a graph has k vertices such that ............................, then the original graph doesn´t have a Hamiltonian cycle.

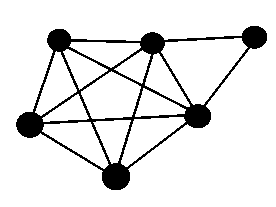
k) (Challenge, Extra Credit) Could the following graph be the G₁ graph of some floorplan of a one story building? Why or why not?