Examples for the notion of duality
A convenient way to think of duals is by the
incidence matrix of H,
where the columns are labeled by the elements of
A and the rows by the elements of V,
and there is a `1' (or `*`, as in the figures) in row
x and column a if
a 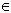 Sx,
otherwise there is a `0`.
Thus the rows `correspond' to the hyperedges of H.
Sx,
otherwise there is a `0`.
Thus the rows `correspond' to the hyperedges of H.
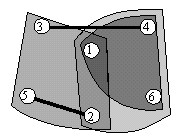
We give a hypergraph by its list of hyperedges, as
Venn diagram, and by its incidence matrix.
| S1={ |
A, |
|
C, |
D, |
|
} |
| S2={ |
|
B, |
C, |
D, |
|
} |
| S3={ |
|
|
C, |
|
E, |
} |
| S4={ |
A, |
|
|
D, |
E, |
} |
| S5={ |
|
B, |
C, |
|
|
} |
| S6={ |
A, |
|
|
D, |
|
} |
|

|
|
A |
B |
C |
D |
E |
| 1 |
* |
0 |
* |
* |
0 |
| 2 |
0 |
* |
* |
* |
0 |
| 3 |
0 |
0 |
* |
0 |
* |
| 4 |
* |
0 |
0 |
* |
* |
| 5 |
0 |
* |
* |
0 |
0 |
| 6 |
* |
0 |
0 |
* |
0 |
|
By transposing the matrix, the roles of columns and vertices
are interchanged.
The dual H* is the hypergraph whose incidence matrix
equals the transpose of the incidence matrix of H.
Now the dual of the hypergraph above is described as follows:
|
1 |
2 |
3 |
4 |
5 |
6 |
| A |
* |
0 |
0 |
* |
0 |
* |
| B |
0 |
* |
0 |
0 |
* |
0 |
| C |
* |
* |
* |
0 |
* |
0 |
| D |
* |
* |
0 |
* |
0 |
* |
| E |
0 |
0 |
* |
* |
0 |
0 |
|
| A*={ |
1, |
|
|
4, |
|
6, |
} |
| B*={ |
|
2, |
|
|
5, |
|
} |
| C*={ |
1, |
2, |
3, |
|
5, |
|
} |
| D*={ |
1, |
2, |
|
4, |
|
6, |
} |
| E*={ |
|
|
3, |
4, |
|
|
} |
|
|
The
intersection graph of the first hypergraph is
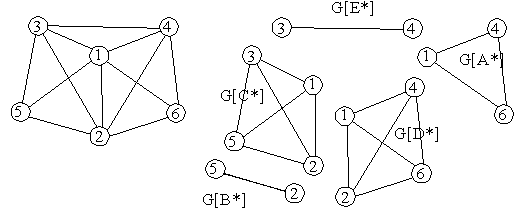
Back to the
start page for intersection graphs.
Erich Prisner
made on January 12, 1999
![]() Sx,
otherwise there is a `0`.
Thus the rows `correspond' to the hyperedges of H.
Sx,
otherwise there is a `0`.
Thus the rows `correspond' to the hyperedges of H.


