Footnotes on 2.4

A few more remarks

• Two numbers are equivalent modulo m if their difference is a multiple of m.
• Every integer is equivalent (mod m) to one and only one of the numbers 0, 1, 2, ... n-1. Thus this set 0, 1, ... m-1 represents all integers mod m.
• If a ≡ b (mod m), then a+c ≡ b+c (mod m) and a-c ≡ b-c (mod m) and also a·c ≡ b· c (mod m). Sums, differences, and products where corresponding parts are equivalent modulo m are equivalent modulo m.

Multiplication by a fixed number modulo m

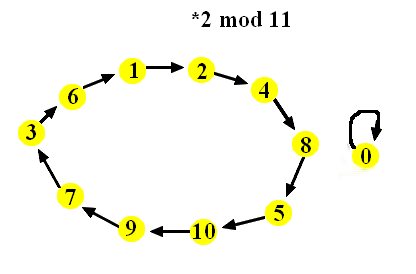
Let us visualize multiplication by 2 modula 11 in the following way: We draw all numbers from 0 to 10 as vertices, similar as for graphs. Remember that every integer is equivalent to some of these numbers modulo 11. Then we draw a directed arc from a to b, a → b, if 2·a ≡ b (mod 11). For instance, 1 → 2, 2 → 4, 4 → 8, 8 → 5 (since 16 ≡ 5 (mod 11)), 5 → 10, 10 → 9, but also 0 → 0. The resutling structure, shown to the right for our example, is called a directed graph or digraph, it is like a graph where all edges are made one-way. Note that at every vertex one arc starts. In our example, one arc also ends at every vertex.

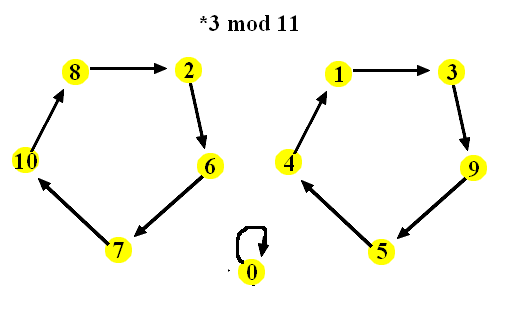
The digraphs for multiplication by 3 or 4 modulo 11 look a little different. But note that even in these two examples one arc ends at every vertex.

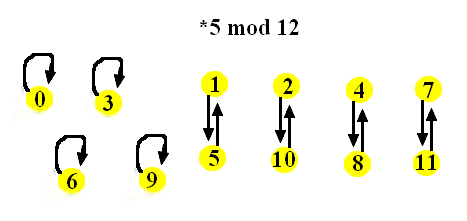
The digraphs for multiplication by 2, 3, 4, and 5 modulo 12 are shown below. Only in the "*5 mod 12" digraphs at every vertex one arc ends. The other three digraphs have some vertices where more than one arc ends, and some where no arc ends. Why?

Below are a few more digraphs. Can you tell in which case we have the property that at every vertex one arc ends?

Solutions of equations modulo m

Is there a solution to the equation 4 · x ≡ 7 (mod 11)? How do we find such a solution? Is there always a solution for the equation
a · x ≡ b (mod 11)
for all numbers a and b? Is there always a solution for the equation
a · x ≡ b (mod 12)
for all numbers a and b? What do these question have to do with what we discussed in the previous section?