MINI LE HER 2(q,k):
This game is played with a q+k cards deck, q Queens and k Kings.
Ann and Beth get both randomly a card at which they look without showing it to their opponent.
A third card is put, back up, on the desk. Now Ann can decide whether she wants
to change cards with Beth (of course without knowing what card Black has).
Next Beth has the opportunity to exchange her card with that lying on the desk.
Now both players reveal their cards, the one with the higher one wins 1 unit from the other.
In case of a tie nobody gets any payoff.
The extensive form of the case q=k=4 is shown below:
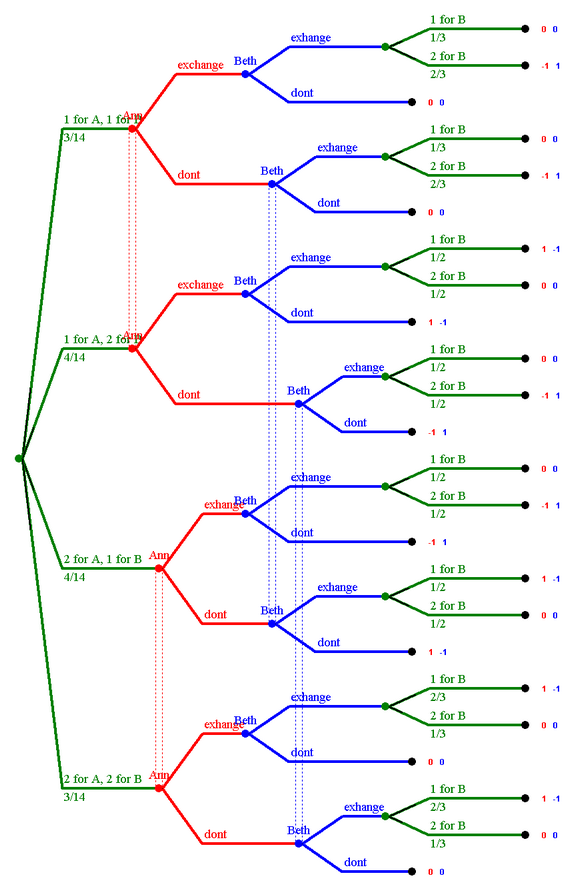
Ann has two information sets, holding a Q or a K, with two moves each,
therefore she has four pure strategies "EE", "ED", DE", and "DD", where "E" stands for
exchange and "D" ("don't") for no exchange.
Beth has six information sets: Holding a "Q" with Ann having a "Q",
or holding a "Q" with Ann holding a "K",
or holding a "K", with Ann holding a "Q", or holding a "K" with Ann holding a "K",
or holding a "Q" and not knowing what Ann has (since she didn't exchange),
or holding a "K" with not knowing what Ann holds (since Ann didn't exchange).
In each of these six information sets she has two options, "E" and "D",
therefore Beth has 2
6=64 pure strategies. Therefore the normal form of the game is
a 4 × 64 matrix.
However, the game has four perfect-information-subgames
which can be analyzed easily using Backwards Induction. They start at the four
positions where Beth has to move and knows both of their cards since Ann has exchanged.
In each of these cases it is clear what Beth has to do.
We cut these subgames, and put the expected payoffs in to
get the following truncated extensive form:
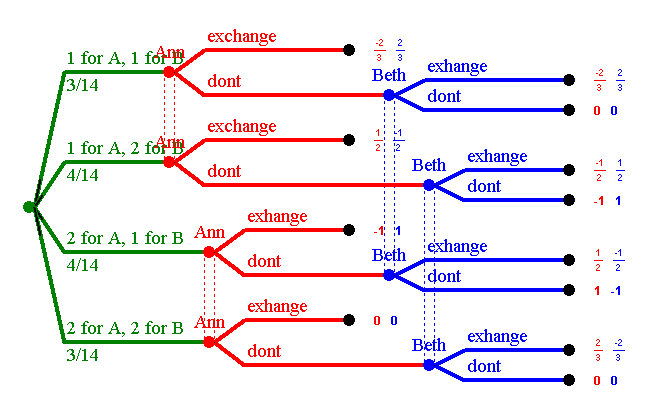
Here Beth has only two information sets left, and four pure strategies:
"EE", "ED", "DE", and "DD". We get the following 4 × 4 matrix as normal form:
| | EE | ED |
DE | DD |
| EE | -2/7 | -2/7 | -2/7 | -2/7 |
| ED | 2/7 | 1/7 | 3/7 | 2/7 |
| DE | -4/7 | -5/7 | -3/7 | -4/7 |
| DD | 0 | -2/7 | 2/7 | 0 |
MINI LE HER 3(j,q,k):
This game is played with a j+q+k cards deck, j Jacks, q Queens and k Kings.
Ann and Beth get both randomly a card at which they look without showing it to their opponent.
A third card is put, back up, on the desk. Now Ann can decide whether she wants
to change cards with Beth (of course without knowing what card Black has).
Next Beth has the opportunity to exchange her card with that lying on the desk.
Now both players reveal their cards, the one with the higher one wins 1 unit from the other.
In case of a tie nobody gets any payoff.
