
In the chapter we look at another class of rather simple games, namely sequential games. These are games where the players move one after another, no two players move at the same time. Among sequential games we concentrate on games of perfect information, where every player knows all previous decisions when he or she moves. Randomness will also only be included after the next chapter. We will learn a little terminology, see how to display these games either as game tree or game digraph, and how to analyze them using the tool of "backward induction" provided the game is finite. We conclude the chapter by discussing whether this solution found by backward induction would really always be what real players would play, by discussing another approach for sequential games and discussing the special roles two-person zero-sum games play here, and also by discussing briefly several existing sequential games like chess, checkers, tic-tac-toe. We also mention a rather simple approach how one would play if not knowing how to play.
A sequential game, is a game where the players move one after another; never are two players supposed to move at the same time. Remember that a position is usually any situation where a player has to make a move, a decision, out of a number of possible moves. Therefore in a sequential game such a position is linked to just one of the players. Later, when we allow randomness, positions may also be situations where a random experiment is performed, so later positions may also belong to the random player. In addition to these positions belonging to some player, there are also positions where the game ends, these are called end positions. They are the outcomes, and obviously nobody is supposed to move then anymore. But at these end positions, the payoff for each player must be given. Every game starts with one and only one start position.
Note that the relevant information known to the player about to move is also part of the position. Usually in a sequential game of perfect information this information is just the sequence of all previous decisions of the other players in all previous moves. If this differs, we usually also have different positions, except in cases where this difference is not relevant for the future. We will explain this more thoroughly below when we explain the difference between Game Trees and general Game Digraphs.
In this chapter we assume perfect information and don't allow random moves. Perfect information means in the context of sequential games that every player will immediately recognize in which position the game presently is.
The game changes its position by moves of players. At each non-end position, the player linked to that position chooses one of his or her possible moves. These possible moves are also known to everybody. Each of these possible moves of the player to move leads to another position.
Sequential games are usually visualized or even described graphically: For each position a small circle is drawn on the paper, and the possible transitions between the positions are expressed by an arrow between the corresponding circles. Very often, instead of arrows one uses straight lines or even curves, from left to right or from up to down, with the convention that the direction is leftwards (in the first case) or downwards (in the second). We usually use lines from left to right. The small circles are usually denoted as vertices or nodes, and the arrows are denoted as arcs. These vertices and arcs are usually labeled. At each non-end vertex, there is a label indicating to whom the vertex belongs, The outgoing arcs of a non-end position correspond to the possible moves the player can make at this position. They are labeled by the move names. The end positions are those vertices with now outgoing arcs---at them the payoffs for each player have to be noted. The whole (directed) graph with all labels is called the Game Digraph or Extensive Form of the sequential game. But note that we need to extend the definition further later, when we take randomness and non-perfect information into account.

Let us look at another example:

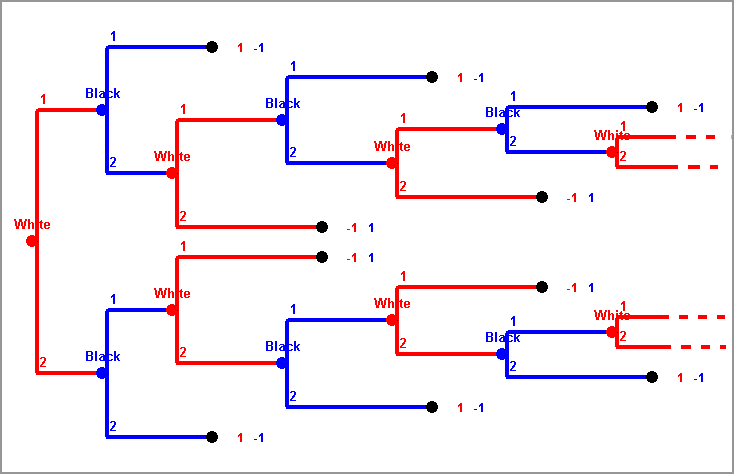
The Extensive Forms in the previous two examples are so-called Game Trees. Let's avoid the formal definition and just say that a Game Tree looks like a tree, rotated by 90 or 180 degrees. Trees arise if one considers a position to be the whole sequence of previous decisions made by all the players who have moved so far.
But in the previous example, it is also obvious that there is some redundancy. Why do we have two "3w" positions? Granted, both have a different history, one resulting from position "5b" with Black taking two stones, and the other from position "4b" with Black taking one stone. But that is not relevant for the future, as can be seen in the Game Tree by the fact that both subtrees hanging at the corresponding vertices are identical. So if White decides how to play in these two positions, he or she should come to the same conclusion.

It should have become clear from the previous discussion that games may have different descriptions by Extensive Forms. We will see more examples later. Note also that in the literature mostly game trees are used to describe extensive forms. Our approach of game digraphs has the advantage of reducing the number of positions.
Next we will discuss a simple and very powerful method how to analyze sequential games. However, this method works only for so-called "finite games". A sequential game is finite if it has a game tree with finitely many vertices. Having a Game Digraph> with finitely many vertices is not sufficient, as can be seen in the next example:
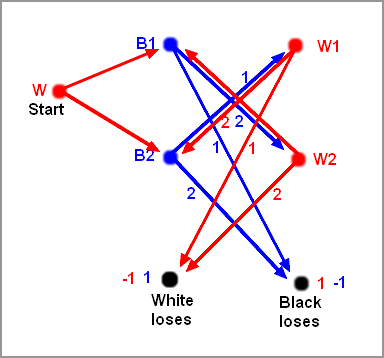 We can also use a Game Digraph. Then a non-end position is uniquely determined by who is about
to move, White or Black, and how many fingers were last shown.
So we have four of these positions, labeled as W1, W2, B1, and B2.
Of course there is one more
position, the start position with White to move, where no fingers have been shown yet,
and two end positions,
one where White wins and one where Black wins.
We can also use a Game Digraph. Then a non-end position is uniquely determined by who is about
to move, White or Black, and how many fingers were last shown.
So we have four of these positions, labeled as W1, W2, B1, and B2.
Of course there is one more
position, the start position with White to move, where no fingers have been shown yet,
and two end positions,
one where White wins and one where Black wins.
Why does the previous example have a finite game digraph although the game is not finite? The reason is that the game digraph is cyclic. That means that it is possible to follow arcs from some vertex x and reach the vertex x again after some time, like in W1, B2, W1 in the above example. Games with a cyclic game digraph have always an infinite game tree, but a sequential game is finite if it has some acyclic (not cyclic) finite game digraph. Why does the previous example have a finite Game Digraph although the game is not finite? The reason is that the Game Digraph has cycles. It is possible to follow arcs from some vertex x and reach the vertex x again after some time, like in W1, B2, W1 in the above example. Thus a sequential game is finite if it has some acyclic finite Game Digraph.
There are theoretical reasons why we exclude these infinite games, but of course there are more practical reasons: We need to have a guarantee that a game eventually ends. Note that even chess would not be finite, were it not for the "50-move rule" that says that a chess play ends as draw if no pawn has been moved within 50 moves.
What players may want from Game Theory is advice how to play. In a sequential game that means that for every position that is not an end position the player who has to move there would need advice about which of his or her possible options to choose. Such a list of recommendations for all the player's positions---even for those positions for which we are rather certain that they will never occur in a play--- is called a pure strategy for that player. In this section we will present a procedure generating pure strategies for all players. Moreover, at each vertex some numbers will be attached by the procedure: the likely payoffs for each one of the players. The word "likely" has nothing to do with probabilities, which will only be discussed in the next chapter. Its meaning here will be discussed later.
Let us explain the method first at another example, this time a non-zero sum game with three players:
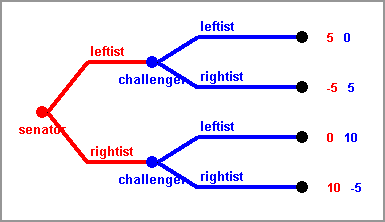
SEQUENTIAL LEGISLATORS VOTE: Three legislators vote whether they allow themselves a salary rise of $2000 per year. Since voters are observing, a legislator would estimate the loss of face by having to vote for a rise as $1000 per year. In the sequential variant considered, A has to vote first, then B, then C, and all votes are open. (This is a variant of a game described in [Kaminski].)

The Game Tree of this game is shown to the right. The behavior of legislator C is easiest to explain first, since at the time when C has to move, A and B have already moved. So C doesn't need to anticipate their strategies. C may face four different situations, corresponding to the four vertices to the right of the tree. In the first situation, when A and B have already voted for a raise, C can keep face by voting against the raise but still get the benefit of it. The same is true if A and B both rejected the idea of a raise and it is decided already. It is different if one voted for and one against a raise. Then C's vote counts. Since the money is more important than face (for our fictitious legislators only!) C would vote for a raise in that case.
Now everybody can do this analysis, therefore if B has to decide, she can anticipate C's reactions. If A voted for a raise, B knows that C will vote for a raise if she votes against, and conversely. So why not give C the burden of having to vote for the raise? Obviously B will vote against a raise in this situation. If on the other hand A voted for a raise, then B has to vote for a raise to keep things open.
Since A knows all this too, A will vote against a raise, B will vote for it, and C will vote for it as well. A has the best role in this game. Going first is sometimes useful, after all!
This method of attaching a recommendation and "likely" payoffs for all players to all vertices of the Extensive Form, starting at the vertices "late" in the game and moving backwards is called "backward induction". We will explain it more formally below.
Note that when a player accepts these decision found by backward induction, he or she must assume that the other players will also stick to these backward induction recommendations. And why wouldn't they? Well, one reason could be that they are not able to analyze the game, since the game is maybe too complicated. Or a player can analyze the game, but doubts that all others can do so.
Procedure for Backward Induction : Your goal is to have likely payoff values for each player assigned at every vertex. As long as not all vertices have such values attached, do the following:
There is still one problem in this procedure. What do we have if there are ties, if two or more successor vertices of a vertex have the same likely payoff for the player to move at that vertex. This case will be discussed in Section 3.4
In 1913, Ernst Zermelo showed that finite perfect-information sequential games can always be analyzed using backward induction. Actually he referred to chess, but this result can easily be generalized to the following:
By construction, the outcome generated by backward induction obeys the following property, which of course has some conncetion to the Nash equilibrium definition:
Although the backward induction solution seems to be the best the players can do in many situations, there are certain sequential games where players tend to play differently:
CENTIPEDE GAME: In this game, two players alternately face two stacks of money. A player to move has the choice either to pass, in which case both stacks grow slightly and the other player faces them, or to take the larger stack, in which case the other player gets the smaller one and the game ends. The game ends anyway after a fixed and known number of rounds, in this example after six rounds.

This game was introduced by Rosenthal [Rosenthal 1981] in the 100 rounds version. It has a unique backward induction solution: Player 1 would take the money in the first round and end the game. On the other hand, players can both increase their payoff if they both wait much longer. When McKelvey and T. Palfrey made experiments with this game [McKelvey, T. Palfrey 1992], they observed that players tend to play some rounds before somebody cannot resist any longer and takes the higher stack.
Here is another classical example:
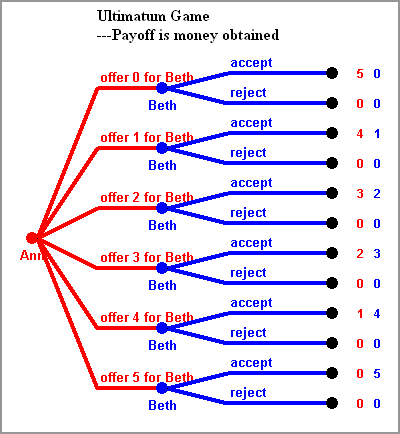
ULTIMATUM GAME: There is a fixed number, say 5, of dollar bills for both players. Ann makes an offer how to share it, which Beth can either accept or reject. If she accepts, the bills are divided as agreed upon, if she rejects nobody gets anything.
The graph to the left shows the extensive form of the game when payoffs mean the money obtained. In the backward induction solution Ann would offer only one bill, or maybe even none---we will discuss this problem with payoff ties in a later subsection---to Beth. However, experiments show that people tend to be less mean than they could. People like to be fair.
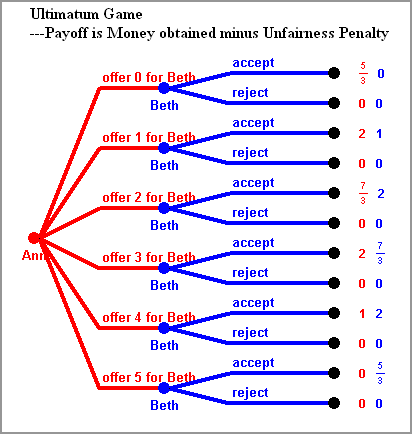
Let us try to model dissatisfaction of unfairness in the following way: Let the payoff of each player not be just the money obtained, but rather express satisfaction about the outcome. Assume this satisfaction is the money obtained, but reduced by an "unfairness penalty" for the player obtaining more. Assume this unfairness penalty is two thirds of the difference between both values. That means that the money exceeding the amount the other gets is still valuable, but only one third of this surplus money satisfies. Then the payoffs of this modified Ultimatum Game can be seen in the figure to the right. The backward induction solution is Ann offering two bills to Beth, which she accepts.
Working through the material so far, you may be a little fed up by these "rational players". It may appear to you rather cold, inhuman even. Granted that companies, aiming to maximize profits, can be modeled by rational players, and granted that in parlor games, in particular in those which are zero-sum, player may only look at their own payoff. But don't we humans, in real-world situations, (hopefully) care about each other? Doesn't that mean that we are not only looking at our own payoff, that we are not indifferent about the other's payoffs?
Does it? Things may become a little clearer if we separate the money paid and the satisfaction received. Let us denote by "payoff" this satisfaction for each player, rather than the money received. This payoff depends on the different features of the outcome obtained, including the money given to the different players. Moreover this dependency on these features, very often called "utility function", is a very individual one, different for every player. Only in the case of a very selfish player the payoff or satisfaction received may be identical to his or her own money won. The payoff of a totally altruistic player may be the sum of the money won by all the other players. And of course, there are possibilities between. In this way, altruism, as well as emphasis towards others, sympathy or antipathy, can be modeled. And in most cases the utility function is not linear---Winning twice the money doesn't make you twice as happy, an idea that will be further discussed in a later chapter.
A player will only get the payoff predicted by backward induction analysis if all players play rationally, i.e. stick to the backward induction analysis moves themselves. Thus this "likely" payoff is not guaranteed: if the other players deviate from backward induction moves, a player may get much less. Therefore using these backward induction moves may be risky. If you want to play it safe, maybe assuming that all others do intend to just hurt you, like in the Maximin paradigm discussed in the previous chapter, you may want to play different moves. See the next example:
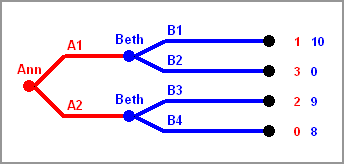 In this game Ann owns one position, the start position, and there are two positions
where Beth is supposed to move, and there are four end positions.
In this game Ann owns one position, the start position, and there are two positions
where Beth is supposed to move, and there are four end positions.Sequential games with perfect information have guaranteed payoffs, also called security levels, for all players. These can be found for every player separately, doing a variant of backward induction, which will be called Security Level Analysis. Let's call the player in question Ann. During this analysis we also find what moves Ann would choose in each of her positions if she would fear that everybody is just playing to hurt her. The resulting strategy is called her Security Strategy. Since this is a completely egocentric point of view, taking only the payoffs for Ann into account, we can eliminate all other payoffs for this analysis. Then we attach a value, the guaranteed payoff for Ann, to every position, starting again at the end positions. For moves with all successors having already guaranteed payoffs for Ann attached, we choose the lowest of these values as the value for the position provided Ann does not move at that position, and the largest of these values of the successors provided Ann does move at that position. In that case Ann will choose the option leading to a position with maximal guaranteed payoff for Ann attached.
This fact gives tremendous significance to backward induction in the two-player zero-sum case. Therefore it seems justified to call the two backward induction strategies of the two players "optimal". If both players, Ann and Beth, stick to these strategies, they will obtain the values attached at the start position as payoffs. If one of them, let's say Beth, deviates, we already know that Beth will get not more. This is even true without the assumption of two-players zero-sum games. But with this additional assumption, if Beth deviates we also know that Ann will not get less, provided Ann sticks to her backward induction strategy.
What happens in the backward induction procedure above if in step (P3) there are two or more successor vertices, let's say "W" and "U", giving both the maximum value for player X to move? Player X would be totally indifferent whether to move to W or to U. The value for X at V is obviously the value for X at W (which is the same as the value for X at U), but still the decision where to move would influence the payoffs of the other players. The most natural solution to these problems is to assume that X will move to W or U with equal probability. This is already a so-called "behavior strategy"---at certain vertices a player would not be determined what to play but rather alternate two or more moves in a random way. Then we call X a "neutral" player. Obviously the value for any other players at V would be computed as the average (expected value with 50-50 probabilities) of the values for that player at W and U.
In a two-person game, a slightly different approach could also be taken. If player X is slightly "hostile" against her opponent, she would choose that vertex of W and U that has the lower value for her opponent. If X is slightly "friendly" she would choose that vertex of W and U that has the higher value for her opponent. Note that she still cares only about her payoffs, only in a tie situation of her own payoff she would consider the other's payoff. Hostile players can be modeled by subtracting a small fraction (let's say 0.1%) of her opponent's payoffs from her payoffs, a fraction so small that the ordering of the payoffs is not changed, only in case of ties suddenly the situations are ordered. Similarly, a friendly player would add a small fraction of the opponent's payoffs to her own payoffs.
Friendly players are far from being altruistic. However, altruistic behavior can also be modeled using the same trick, but for real altruism one would add a considerable amount of the opponent's payoff to the player's own payoff.
There are even more ways of breaking ties, also for more than one player. A player may be friendly to some players and hostile to others. Backward induction analysis must be changed in each of these cases.
In real life, where the rules are not always carved in stone, two players playing a simultaneous game may have the possibilities of either moving a little earlier than the other, or delaying their move slightly until they see what the other player played. Even if moving earlier is not possible, sometimes it is possible to publicly announce what you will play, to make a (hopefully convincing) commitment. If the other player believes you, it is as if you would have moved first. In any case, the former simultaneous game is transformed into a sequential game.
Obviously there are two roles in the sequentialization of a two-player game, moving first or moving second, and which one is preferred is probably often decided by the temperament of the players. Some like to move first and dictate the action, and others prefer to wait and see what the other has played, leaving the other in the dark about their intentions. But actually this question of whether it is better to move first or last in a sequentialization should not be left to temperament but to an analysis of the game.Backwards analysis of the sequential version carries over to bimatrix notation quite easily: If Ann moves first and Beth second, then Ann determines the row with her move. Each row corresponds to a situation Beth may face, and in each row, Beth obviously would choose the cell maximizing her payoff. This is her best response to Ann's move. We color all these cells. Note that the colored cells include all pure Nash equilibria, since the condition for coloring is just one of two (both moves being best response to the other) required for pure Nash equilibria. Note also that every row contains at least one colored cell.
The simplest case is where in each row only one cell is colored. We call this property unique response for Beth. That means that every one of Ann's moves has exactly one best response. In this case, Ann chooses the row whose colored cell has maximum first (Ann's) entry. Similarly, unique response for Ann would mean that in every column there is exactly one entry maximizing Ann's payoff.
If there are more than one colored cell in a row, Ann chooses the row with
using the three variants to break ties discussed in the previous section.
Let's apply the Theorem to the game CHICKEN. The classical formulation is of two cars driving at each other. We assume that it is a simultaneous game; both have at some point to decide simultaneously whether to proceed or to swerve. The one swerving loses face. If none swerves, both lose their lifes.
| swerve | not | |
| swerve | -1, -1 | -2, 2 |
| not | 2, -2 | -100, -100 |
Very often the first condition fails. People are often indifferent between options. But if we assume that Beth decides in these cases looking at Ann's payoff, as discussed in the previous subsection, this first condition is valid. The second condition is necessary since presently we don't have a solution concept yet if there are no Nash equilibria in pure strategies. Later, when we allow and discuss mixed strategies, we will see whether this condition remains necessary. The third condition makes it possible to compare Ann's and Beth's payoffs.
Look at the following symmetric game, where both player's moves are called "1", "2", and "3". The colored cells are the outcomes with best response for Beth:
| 1 | 2 | 3 | |
| 1 | 1, 1 | 3, 2 | 3, 1 |
| 2 | 2, 3 | 4, 4 | 2, 4 |
| 3 | 1, 3 | 4, 2 | 2, 2 |
What happens in the same game with hostile or friendly Beth?
| hostile Beth | friendly Beth | ||||||||||||||||||||||||||||||||
|
|
Another example where the Theorem cannot be applied since the assumptions are not there is ROCK-SCISSORS-PAPER. It has unique best response for Beth and is symmetric, but it doesn't have any Nash equilibria in pure strategies. In fact, there is a second move advantage there---you would rather want to move slightly later than your opponent there.
Board games are, almost by definition, games of perfect information, since everything is in the open provided no cards are part of the game. They are also very often sequential games, where the players take turns to move. Well-known example of board games are Chess, Go, Nine Men's Morris, Checkers, Pachisi, Backgammon with a very long history, or the more recent games of Monopoly, Hex, Tic-tac-toe or others. Some, like Pachisi, Backgammon, and Monopoly, are played with dice or even with cards that are revealed, and contain therefore randomness. But Chess, Go, Checkers, Tic-tac-toe, Hex are all two-players zero-sum finite sequential games without randomness and with perfect information. So shouldn't people play the backward-induction strategy? The simple and quick answer is: Yes, they should, but in some cases backward induction analysis has just not yet been performed. Thus the backward induction strategy, the optimal strategy, is unknown in many cases.
Tic-tac-toe is the simplest of these games, with the smallest game tree. The game tree has just 5478 positions. The game has been analyzed, and the expected outcome is a draw. You can play tic-tac-toe here against the computer.
Checkers will always result in a draw when played correctly ([von Nievergelt and Gasser 1994].
On the other hand, for Chess and Go the number of possible positions is so large that even with the help of the most advanced computers a full analysis is not expected for soon. Chess has about 1043 positions, a number with about 43 digits, and Go even about 2·10170. Checkers has about 1018 positions and Nine Men's Morris about 1010 positions.
How do chess computers play? We have already seen that the complete extensive form is not available---it is simply too large. Therefore backward induction is also not an option. These existing chess programs usually have two ingredients: Starting at a position, they look a few moves ahead, instead of looking back. Secondly a chess program, the same as an experienced chess player, has values attached, or can attach values, to every possible position. They are supposed to be approximations of the likely payoffs found by backward induction, but they are not obtained by looking any further to successors of the position considered. Rather features of the position are considered and expressed into a value using a more or less complicated formula. In chess, material advantage are part of these features to consider, but there are also finer features, like the number of possible moves of a position, or pawn structure, and so on.
Very often such evaluations of positions come very naturally. For instance, for many games the evaluations might be the payoff if the game just ended there.
Now a Greedy strategy decides what to do in a position by simply looking at all possible successor positions, and choosing the one where the evaluation for the player to move is highest. More generally, a k-Greedy strategy looks just k moves ahead, and chooses the Maximin or backward induction choice of this small part of the Game Digraph.
Nash showed in 1948 that in Hex White always must win, even though it is not known how. The proof is called a strategy-stealing argument.
Actually deciding whether a given position is a winning position for White or Black is fairly difficult (PSPACE-complete, TIME??? Nachgucken! ) [Reisch 1979]. That means that it is fairly unlikely to have an algorithm that solves this decision problem in reasonable time. But maybe it's not important enough.