Homework 3
Homework 3 2008 DMA Soccer, Sequential Games with Randomness,
This question refers to
DMA soccer discussed here.
Assume each team has six players,
and A has three defence, two midfield, and one attack players,
and Beth has 2 defence, 2 midfield, and 2 attack players.
- a) What is the probability of a goal for team A in a round?
- b) What is the probability for a goal for team B in a round?
- c) What is the expected value of goals for team A in a 4-round play?
- d) What is the probability for no goal in a round?
- e) What is the probability for a result of 2:1 for team A in a 4-round play?
- f) What is the probability for a result of 1:1 in a 4-round play?
- g) What is the probability for a draw in a 4-round play?
- a) pA = (2/4)·(1/3) = 1/6.
- b) pB = (2/4)·(2/5) = 1/5.
- c) It is 4 · 1/6 = 2/3.
- d) The probability for no goal at all is p0=1-pA-pB = 19/30.
- e) The goal for B could fall in any of the four rounds. In each of these four cases, the
goalless round could be any of three possible rounds. Thus we have 12 cases of achieving a result of 2:1,
B0AA, BA0A, BAA0, 0BAA, AB0A, ABA0, 0ABA, A0BA, AAB0, 0AAB, 0A0Bm 0AAB,
where "A" denotes a goal for A, "B" a goal for B, and "0" the round without a goal.
The probability for each of these 12 outcomes is pA2·pBp0
= (1/6)2·(1/5)·(19/30) = 19/5400
These 12 outcomes are all mutually disjoint, therefore the probability for a 2:1 for team A
equals 12·(19/5400) = 19/450 = 0.0422, or 4.22%
- f) This is done in the same way. Again there are 12 ways to obtain a 1:1 in a 4-round game,
depending of when the goal for A falls, and when the goal for B falls.
The probability for each of these 12 outcomes is
p02·pApB
= (19/30)2·(1/6)·(1/5) = 361/27000.
Again these 12 outcomes are mutually disjoint, and the probability for a 1:1 equals
12·(361/27000) = 0.1604, or 16.04%.
- g) There are three ways to get a draw in a 4-round game: 0:0, 1:1, or 2:2.
The probability for a 0:0 is 1·p04 = 16.09%
The probability for a 2:2 is 6·pA2·pB2
= 0.67%
Therefore the probability for a draw is the sum of these three probabilities,
and therefore about 16.09% + 16.04% + 0.67% = 32.80%.
Analyse the
3·3 version of Polynomial REC THE SQUARE
with randomness game.
Explain
what will happen if both play optimally. How much will each of the players expect,
if a win counts a s +1 and a loss as -1?
Note that you can describe the game using the following 27 states,
where each symbol subsumes the cases obtained by rotation and reflection.

The following sequential game with randomness but perfect information
is given in extensive form. There are two players, Ann and Beth.
Vertices are labeled by the player whose turn is it. Vertices without
such a label are random moves, the probabilities for the two options are 50% and 50%
in each case. The payoffs of the end vertices are given, always first Ann's payoff,
then Beth's.
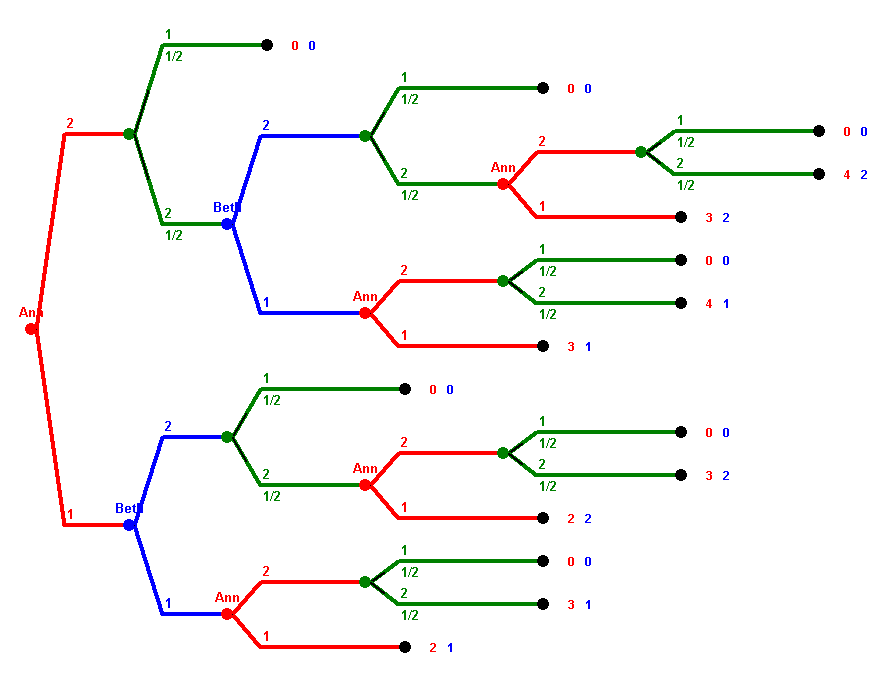
Analyze the game using backwards induction.
- What first move would Ann make when playing optimally?
- What is the expected payoff for Ann in the game when Ann plays optimally?
Here is the solution done by using backwards induction for a "neutral" Beth:

Note that there are a few variants here. The above solution is the case where a player would
randomly chose among moves that yield identical payoffs for here (the neutral player).
Note that in class we also discussed cases where a player, in such a case where two payoffs of two
options for that player are identical, would look at the opponent's payoff as second (minor criterium).
A friendly player would try to give the opponent the best possible (all under the condition
that for her own payoff it doesn't matter), and a hostile player would try to minimize it.
In the game above, Beth is in both situations indifferent about her moves.
A friendly Beth would play "1" in both cases, a hostile Beth would play "2" in both cases,
a neutral Beth alternates. Whether or not Ann is friendly or neutral or hostile doesn't matter.
If Beth is friendly, then the values of the game are 2 for Ann and 1 for Beth.
If Beth is neutral, then they are 1.5 for Ann and 1 for Beth, and they are 1 for both
in case of a hostile Beth. In all these three cases, Ann would start the game by playing "1".
Consider the following game:
KUHNPOKER: We play with a 8 cards deck, four "1"s and four "2"s.
Every player gets one card and looks at it secretly.
The start bet is $2.
Ann moves first by either checking or raising.
- If Ann checks, then Beth can check or raise.
- If Beth checks, both cards are revealed and the player with the higher card wins the pot of $4.
splitting it again equally in case of a draw.
- If Beth raises, she increases the bet to $3. Then Ann has two options,
she can either fold or call.
- If Ann folds, Beth gets the pot money of $5, i.e. wins $2.
Ann's card is not revealed in that case.
- If Ann calls, she also increases her bet to $3. Then both cards are revealed again,
and the player with the higher card gets the money of $6, i.e. wins $3. Again, in case of a draw
the money is split equally.
- If Ann raises, she increases the bet to $3. Then Beth has two options,
she can either fold or call.
- If Beth folds, Ann gets the pot money of $5, i.e. wins $2.
Beth's card is not revealed in that case.
- If Beth calls, she also increases her bet to $6. Then both cards are revealed again,
and the player with the higher card gets the money of $6, i.e. wins $3. Again, in case of a draw
the money is split evenly.
Draw the extensive form of the game. How many pure strategies does Ann have,
and how many pure strategies does Beth have?

Since Ann has 4 information sets with
two moves possaible in each, she has 16 pure strategy.
The same holds for Beth.




