Advanced Topics:

Differentiating inverse functions

Assume the functions f and g are inverse to each other, i.e. g = f^-1 and f = g^-1. How can we get the formula for the derivative g' of g using the formula for the derivative f' of f?

Note that the graph of f is the reflection of the graph of g along the "mirror" line y=x. Therefore, reflecting the tangent to g at x₀ we get the tangent to f at y₀ = g(x₀), see the pictures to the right. f (f(x)=(x^2-2*x+2)/(1-x)) is displayed in red, and g in green/yellow. The tangent to g at x₀=2.5 is blue, whereas the tangent to f at y₀=0.5 is pink. The mirror is black.

Since the two tangent are mirrors of each other, they are inverse functions. If the tangent to g at x₀ has the equation y=mx+b, then the tangent to f at y₀ has the equation x=my+b, or y = x/m-b/m. in otehr words, the slopes of the two tangents are reciprocals of each other. Since the first slope (m) equals g'(x₀), and the other is f'(y₀) we get

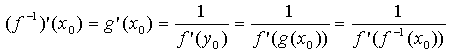
Here you can find a MathCad sheet allowing you to display a function together with its inverse function and tangents.

Another way of deriving the formula above is to start with f(f^-1(x))=x and differentiate both sides. With the chain rule you get f'(f^-1(x))*f^-1'(x) = 1, which directly leads to the equation above.

Erich Prisner, October 2003