 MAT37x
MAT37x
Franklin College
Spring2004
Erich Prisner,
 MAT37x
MAT37x
Franklin College
Spring2004
Erich Prisner,
 The Cassini surface is a function from
R2
into
R.
Actually there are many such surfaces, for each parameter b one.
f(x,y) is defined to be the product of both distances from the point
(x,y) to (b,0) and to (-b,0).
(note that if it would be defined as the sum of these distances, we would get a surface with ellipses as level lines).
Since the distance between (x,y) and
(b,0) equals the square root of
(x-b)2+y2, we get
The Cassini surface is a function from
R2
into
R.
Actually there are many such surfaces, for each parameter b one.
f(x,y) is defined to be the product of both distances from the point
(x,y) to (b,0) and to (-b,0).
(note that if it would be defined as the sum of these distances, we would get a surface with ellipses as level lines).
Since the distance between (x,y) and
(b,0) equals the square root of
(x-b)2+y2, we get
We will always consider only the function f with parameter b=2, thus we get
Here are the partial derivatives:


Obviously these expressions are not defined at the two critical points (-2,0) and (2,0). The level lines of these functions fx and fy are shown below.
Remember that level lines cannot cross. Therefore what looks like a crossing of level lines at (-2,0) and (2,0) only means that these level lines come closer and closer when approaching the two points (where the functions fx and fy are not defined).
Note that the level line of fx of level 0 are all points where the level lines of the original Cassini surface have a horizontal tangent. In our example it is the circle with center (0,0) and radius 2 . In the same way, the level line of fy of level 0 are all points where the level lines of the original Cassini surface have a vertical tangent. In our example it is the x -axis.
The level lines of the Cassini surface are the so-called Cassini curves. Look at the Cassini curve of level h , recall it has the equation:
Using implicit differentiation (use product rule, and remember that y=y(x) depends on x) with respect to x, we obtain

Then we solve this equation for dy/dx and get
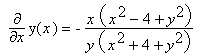
 On the right is the direction field of this first order differential equation. Of course, the solutions are just the Cassini curves---the level lines of the surface.
On the right is the direction field of this first order differential equation. Of course, the solutions are just the Cassini curves---the level lines of the surface.
Remember that another way to obtain dy/dx uses the partial derivatives and the formula dy/dx = -fx/fy. Try it to see that we get the same result.
The gradient has both direction and absolute value. The direction is depicted to the right, it is perpendicular to the direction field shown above. Again we have the connection to differential equations.
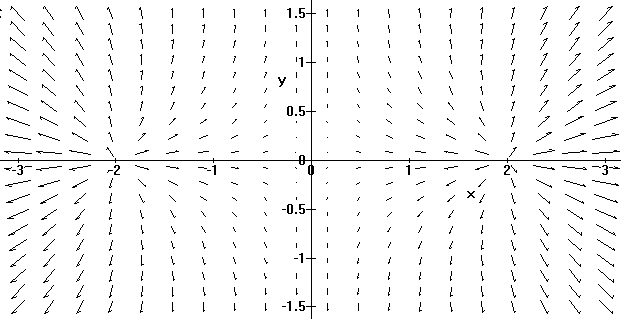
What is the absolute value of the gradient vector (fx,fy)? It is the square root of fx2+fy2. If we substitute the values above and simplify, we get the answer
So the surprising answer is that the steepness of the Cassini surface only depends on the distance of the point to (0,0), it is twice this distance. Therefore there can only be one saddle point---the point (0,0) itself, and there are no local maximum or minimum points, at least not where the function is differentiable. Of course there are two minimum points at nondifferentiable (critical) points (2,0) and (-2,0).