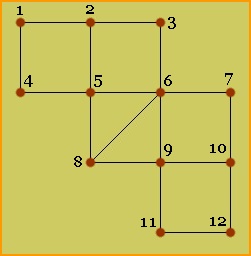
Structures like track structure in the two previous examples are called graphs.
We have the tracks, which are called edges,
and the switches, where two or more edges meet
or edges end. These are called the vertices.
To make them more visible in our example to the right, we marked them by brown dots
and labeled them from 1 to 12.
Edges connect vertices, and two vertices are adjacent if they are connected by an edge. In our example vertices 1 and 2 are adjacent, but vertices 1 and 5 are not.
On graphs we can move from vertex to vertex, step by step, along edges. Such movements are called walks. A walk is a sequence x, y, z, ... w of vertices where any two consecutive vertices are adjacent. If no vertex occurs repeatedly in the sequence, it is called a path. If on the other hand the first and the last vertex of the sequence are identical, but otherwise all others are different, then it is called a cycle. In our example, 5, 6, 9, 8, 6, 3 is a walk, 5, 6, 9, 8 or 5, 6, 7, 10, 9, 11, 12 are paths, and 5, 6, 9, 8, 5 is a cycle.
Obviously every train position forms a path of length 4.