Some Definitions
Formally a graph is a pair
(V,E) where V is any set, called the vertex set,
and the edge set E is any subset of the set of
all 2-element subsets of V.
Usually the elements of V, the vertices, are
illustrated by bold points
or small circles, and the edges by lines between them.
Families
of sets (Sx/x
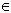V)
are called hypergraphs.
The sets Sx are called the hyperedges,
whereas the elements of the union A of all sets Sx, x V,
are the points or vertices of the hypergraph.
The intersection graph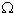 
(H) of a hypergraph
H=(A, (Sx/ x 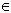V)) has V as vertex set, and two distinct vertices
x,y are joined by an edge whenever Sx 
Sy is nonempty.
Look on an example of a
hypergraph and its
intersection graph.
For every 0-1 matrix
we get a row-intersection graph
whose vertices correspond to the rows,
and where two distinct vertices are adjacent if there is some column
where the corresponding rows both have a `1´.
The intersection graph of a hypergraph is just the
row-intersection graphs of the corresponding
adjacency matrix.
By boxes we mean generalized
rectangles with sides parallel to the coordinate axes,
i.e. subsets {(x1, ... , xd) all
ai
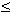xi
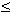bi}.
By cliques we mean inclusion-maximal
complete subgraphs.
The clique hypergraph of a graph has the same vertices
than the graph, and all cliques as hyperedges.
The clique graph of a graph G is the intersection graph
of the set of all cliques of G
(i.e. the intersection graph of the clique hypergraph of G).
Clique-Helly graphs are
graphs whose clique hypergraphs obey the Helly-property
Three vertices form an asteroidal triple
whenever any two of them are connected by a path
avoiding the third and its neighbors.
Three edges form an asteroidal triple if
any two are connected by a path avoiding vertices and
neighbors
of the third edge.
A class H of hypergraphs is
closed under subhypergraphs
if every hypergraph obtained from a member of
H by deleting some hyperedges is again in H.
an induced subgraph of a graph is obtained by deleting
some vertices and all edges incident with one or two of the
deleted vertices.
A class G of graphs is
closed under subgraphs
if every induced subgraph of any member of
G is again in G.
A biclique is any inclusion-maximal
induced
complete bipartite subgraph (where it is even
allowed that one partition class is empty).
Dicliques are ordered variants of bicliques.
The complement
--G of the graph G
has the same vertex set than G,
but two distinct vertices are adjacent in
--G if and only if they are
nonadjacent in G}
The square and the
2-step graph
of the graph G have both the same vertex set than G.
Two distinct vertices are adjacent in the square
if their distance in G is at most 2,
and in the 2-step graph if they have some common neighbor in G.
Erich Prisner
made on January 12, 1999