V),
where the Sx
are 1-element sets and the Tx
are k-element sets, for fixed k,
are almost as easy to recognize, as is left to the reader.
The line digraph L(D) of a digraph D is the intersection digraph of the arc set of D, where an arc is viewed as a pair of vertices. Line digraphs are generally considered as the natural digraph analogue of line graphs. However, recognizing line digraphs is considerably easier than recognizing line graphs---if we do not have loops, we simply have to find all so-called dicliques and essentially compute its intersection digraph to find D. There is no ambiguity, as for line graphs, where we have to find out which triangles are star graphs. If we look closer on the concept, line digraphs are not the analogue of line graphs---instead, they are digraph analogues of unions of complete graphs. Interval digraphs of multigraphs are just intersection digraphs of families of pairs (Sx,Tx), where each Sx and each Tx contains exactly one element. Line graphs of multigraphs are intersection graphs of 2-element sets. Intersection graphs of 1-element sets are just unions of complete graphs.
Intersection bigraphs of pairs of 1-element sets are just unions of complete bipartite graphs. In other words, a digraph D is the line digraph of some multigraph iff its bigraph B(D) is the disjoint union of complete bipartite graphs.
What about discrete intersection bigraph models
where the sets involved are larger?
Intersection bigraphs of families
((Sx,Tx),
xV),
where the Sx
are 1-element sets and the Tx
are k-element sets, for fixed k,
are almost as easy to recognize, as is left to the reader.
Thus the first challenge, and the real bigraph version of line graphs, would be the case where all Sx and all Tx contain 2 elements, all Sx are distinct, and all Tx are distinct. We could view this as intersection bigraphs B of pairs G1, G2 of graphs with the same vertex set.
Obviously all star graphs are complete bipartite, but not all of them are bicliques. On the other hand, there are several other types of bicliques in B, as indicated below:
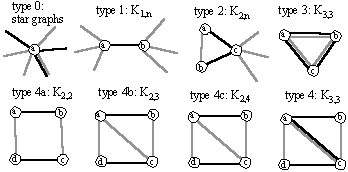
It turns out that the recognition problem is easy if we require large enough minimum degree on both G1 and G2.
Under the condition
(G1),
(G2)
4,
all star graphs are bicliques, and more important,
all bicliques are star graphs.
Then recognition is straightforward.
Let us now relax to the condition
(G1),
(G2)3.
Again all star graphs are bicliques, and there are only two further
types of bicliques, type 3 and type 4 in the
figure above.
Note that every vertex of B lies in exactly two star graphs,
and every edge in one or two of them.
Our strategy is now as follows: First we
compute all large bicliques,
where a biclique is called large if it
contains K3,3.
We compute the intersection multigraph M
of the large bicliques.
All large bicliques are originally unlabeled.
Now we label essentially all vertices of M
by `*', `3', or `4',
depending on whether the biclique is a star graph
or has type 3 or 4 in the
figure above.
Starting with the assumption that
one
particular large biclique B0
is a star graph,
we proceed to label the vertices of M by five rules.
The simplest of them says, that if a vertex labeled by `*'
is connected to another vertex by a
single edge in M,
then this other vertex also gets the label `*'.
If B is indeed a line bigraph with
G1, G2 as above,
and if our assumption on B0
being a star graph was correct,
then we succeed to label almost all vertices of
M correctly.
There remain some `white spots', corresponding to
K2s in
G1
G2,
which however do not harm.
[P°]:
There is a polynomial-time algorithm that decides for any
bipartite graph B whether it is the line bigraph
of a pair (G1,G2)
of graphs on the same vertex set, with
(G1),
(G2)3.
|
Recognizing general line bigraphs is however NP-complete [P°].
Do you want to visit also interval bigraphs, or go back to the start page for intersection graphs?